BELAJAR MATEMATIKA
Sabtu, 25 Maret 2017
Kamis, 23 Maret 2017
KUBUS DAN BALOK
Apa itu bangun ruang sisi datar?
Kelompok bangun
ruang sisi datar adalah bangun ruang yang sisinya berbentuk datar (tidak
lengkung). Coba kalian amati dinding sebuah gedung dengan permukaan sebuah bola.
Dinding gedung adalah contoh sisi datar dan permukaan sebuah bola adalah contoh
sisi lengkung. Jika sebuah bangun ruang memiliki satu saja sisi lengkung maka
ia tidak dapat dikelompokkan menjadi bangun ruang sisi datar. Sebuah bangun
ruang sebanyak apapun sisinya jika semuanya berbentuk datar maka ia disebut
dengan bangun ruang sisi datar.
Macam-macam Bangun Ruang Sisi Datar
Ada banyak
sekali bangun ruang sisi datar mulai yang paling sederhana seperti kubus,
balok, limas sampai yang sangat kompleks seperti limas segi banyak atau bangun yang menyerupai kristal. Namun demikian kali ini kita akan membahas spesifik
tentang bangun ruang kubus, balok,
A. KUBUS
Dari gambar diatas dapat disimpulkan bangun tersebut dibatasi oleh 6 buah sisi yang
berbentuk persegi (bujur sangkar). Bangun ruang ini mempunyai 6 buah sisi, 12
buah rusuk, dan 8 buah titik sudut. Beberapa orang sering menyebut bangun ini
sebagai bidang enam beraturan dan juga prisma segiempat dengan tinggi sama
dengan sisi alas.
Perhatikan
gambar kubus di atas ini.
Kubus
ABCD.EFGH dibatasi oleh bidang ABCD, ABFE, BCGF, CDHG, ADHE, dan EFGH.
Bidang-bidang tersebut disebut sisi-sisi kubus ABCD.EFGH. Selanjutnya, AB , BC
, CD , AD , EF , FG , GH , EH , AE , BF , CG , dan DH disebut rusuk-rusuk
kubus.
Berikut
jumlah bagian-bagian kubus
1. Titik
sudut 8 buah
2. Sisi
berjumlah 6 buah (luasnya sama)
3. Rusuk
berjumlah 12 buah sama panjang
4. Diagonal
bidang berjumlah 12 buah
5. Diagonal
ruang berjumlah 4 buah.
6. Bidang
diagonal berjumlah 6 buah
Rumus-rumus Kubus
Volume
= s x s x s = s3
Luas
Permukaan = 6 s x s = 6 s2
Panjang
Diagonal Bidang = s√2
Panjang
Diagonal Ruang = s√3
Luas Bidang
Diagonal = s2√2
keterangan:
s = panjang
sisi kubus
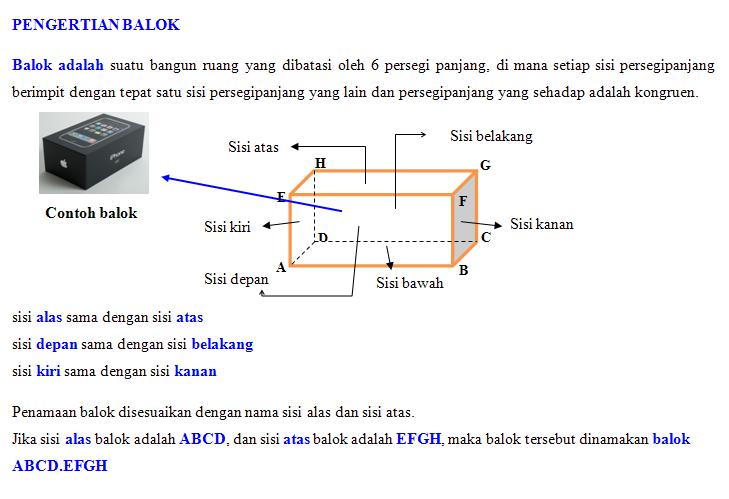
B. BALOK
Coba kalian
perhatikan benda-benda di sekitar kalian, banyak sekali sebenarnya benda yang
memiliki bentuk bangun ruang balok. Kardus mie instan favorit kalian bentuknya
adalah balok, kulkas di dapur rumah juga berbentuk balok. Lantas kenapa
benda-benda tersebut dinamakan balok?
Apa itu balok?
Balok adalah
bangun ruang yang memiliki tiga pasang sisi segi empat (total 6 buah) dimana
sisi-sisi yang berhadapan memiliki bentuk dan ukuran yang sama. Berbeda dengan
kubus yang semua sisinya berbentuk persegi yang sama besar, balok sisi yang
sama besar hanya sisi yang berhadapan dan tidak semuanya berbentuk persegi,
kebanyakan bentuknya persegi panjang. Buat lebih memahami silahkan sobat amati
lagi kulkas di bawah ini.
Perhatikan gambar di atas!
Bagian-bagian
dari bagung ruang sisi datar ini sama seperti bagian-baian kubus. Sebuah balok
terdiri dari sisi, sudut, diagonal bidang, diagonal ruang, dan yang terakhir
adalah bidang diagonal. Berikut rincian jumlahnya
1. Titik
sudut 8 buah
2. Sisi
berjumlah 6 buah (luasnya beda-beda)
3. Rusuk
berjumlah 12 buah
4. Diagonal
bidang berjumlah 12 buah
5. Diagonal
ruang berjumlah 4 buah.
6. Bidang
diagonal berjumlah 6 buah
Rumus-rumus Balok
Volume
= panjang x lebar x tinggi = p x l x t
Luas
Permukaan = 2 (pl + pt + lt)
Panjang
Diagonal Bidang = √(p2+l2) atau √(p2+t2)
atau √(l2+t2)
Panjang
Diagonal Ruang = √(p2+l2+t2)
Luas Bidang
Diagonal = tergantung dari bidang diagonal yang mana
Keterangan:
p = panjang
l = lebar
t = tingi
BANGUN RUANG SISI LENGKUNG
Berbicara
mengenai bangun ruang sisi lengkung, itu berarti kita membicarakan tentang
bola, tabung, dan kerucut. Apakah kalian semua sudah tahu semua rumus –
rumusnya? Nah, kalau belum tahu semua, ayo segera cari tahu, karena kalian akan
ketinggalan apabila dari sekarang belum mencari tahu. Agar kalian tidak
penasaran lagi, langsung simak saja materinya berikut ini.
Pengertian
bangun ruang sisi lengkung
Bangun ruang
sisi lengkung adalah suatu kelompok bangun ruang yang memiliki sisi melengkung,
memiliki selimut atau memiliki permukaan bidang. Seperti yang telah saya beri
tahu diatas tadi, bahwa kelompok bangun ruang yang memiliki sisi lengkung
adalah meiputi bola, kerucut dan tabung.
A. Tabung
Tabung
merupakan kelompok bangun ruang sisi lengkung yang terdapat dua batas berbentuk
lingkaran pada atas dan bawahnya. Kedua lingkaran tersebut berukuran sama besar
serta kongruen. Kedua lingkaran tersebut disatukan oleh persegi panjang yang
melengkung mengikuti sisi kedua lingkaran tersebut. Tabung terdiri dari:
(r) = jari
– jari lingkaran
(t) =
tinggi tabung
Rumus –
rumus yang berlaku pada tabung:
Luas alas
= luas tutup = luas lingkaran = πr2
Luas
selimut tabung = 2πrt
Luas
permukaan tabung = luas alas + luas tutup + luas selimut
= πr2 + πr2
+ 2πrt
= 2πr2 +
2πrt
= 2πr (r +
t)
Volume
tabung = luas alas x tinggi
= πr2t
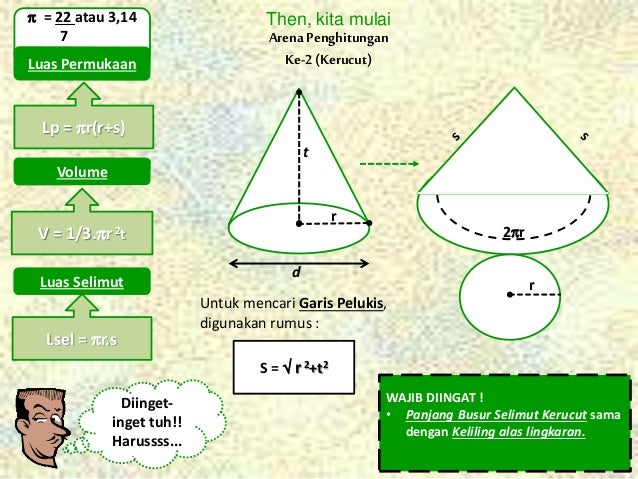
B. Kerucut
Kerucut
merupakan bangun ruang yang memiliki alas berbentuk lingkaran dimana lingkaran
tersebut tutupi oleh selimut yang memiliki ketinggian sejumlah t. Selimut
tersebut diseut garis pelukis. Unsur
unsur yang terdapat pada kerucut adalah:
(r) = jari – jari lingkaran
(t) = tinggi kerucut
(s) = garis pelukis kerucut
(r) = jari –
jari lingkaran
(t) = tinggi
kerucut
(s) = garis
pelukis kerucut
Rumus –
rumus yang berlaku untuk kerucut:
- Luas alas
= luas lingkaran = πr2
- Luas
selimut = πrs
- Luas permukaan
kerucut = luas alas + luas selimut
= πr2 + πrs
= πr (r + s)
Volume
kerucut = 1/3 x πr2t
C. Bola
Bola
merupakan salah satu bangun ruang yang memiliki sisi melengkung dimana terdapat
jari – jari didalamnya. Pajang sisi 1 ke sisi yang lainnya disebut dengan
diameter, atau bisa dikatakan panjang 2r = diameter. Unsur – unsur pada bola
adalah:
- (r) = jari
– jari bola
Rumus –
rumus yang berlaku:
Kamis, 16 Maret 2017
ARITMETIKA SOSIAL
A.Aritmetika
sosial dalam kegiatan ekonomi
1.Menghitung
Nilai Keseluruhan, Nilai Per Unit, dan Nilai Sebagian
Seorang pemilik toko
menjual satu kotak karet penghapus dengan harga Rp8.400,00. Ternyata, dalam
satu kotak terdapat 12 buah karet penghapus. Seseorang membeli sebuah karet
penghapus dan pemilik toko menjualnya dengan harga Rp700,00.
Dalam hal ini, harga satu kotak karet penghapus = Rp8.400,00 disebut nilai keseluruhan, sedangkan harga satu buah karet penghapus = Rp700,00 disebut nilai per unit.
Dalam hal ini, harga satu kotak karet penghapus = Rp8.400,00 disebut nilai keseluruhan, sedangkan harga satu buah karet penghapus = Rp700,00 disebut nilai per unit.
Contoh soal :
Seorang pedagang buah membeli
12 buah durian. Ia membayar dengan 3 lembar uang seratus ribuan dan mendapat uang kembalian
sebesar Rp30.000,00.
a.
Tentukan harga pembelian seluruhnya.
b.
Tentukan harga pembelian tiap buah.
c. Jika
pedagang tersebut hanya membeli 8 buah durian, berapakah ia harus membayar?
Alternatif Peyelesaian:
a. Harga pembelian = 3 x Rp100.000,00 – Rp30.000,00
=
Rp300.000,00 – Rp30.000,00
= Rp 270.000,00
Jadi, harga pembelian seluruhnya adalah Rp270.000,00
.
b. Harga durian per buah =
Rp270.000,00 : 12
=
Rp22.500,00
c. Harga 8 buah = 8 x
Rp22.500,00 = Rp180.000,00
Jadi,
harga 8 buah durian adalah Rp180.000,00.
Latihan 1
1. Tentukan
harga per unit jika diketahui harga keseluruhan berikut ini.
a.
Harga 3 lusin buku tulis Rp 72.000,00.
b.
Harga 1 kodi baju kaos Rp 450.000, 00 ( 1 kodi = 20 buah)
c.
Harga 1 gros jepit rambut Rp 228.000,00 ( 1 gros= 144 buah)
2. Tentukan
harga keseluruhan dari barang-barang berikut ini.
a.
15 bungkus mie instan jika harga perbungkus Rp 2.900,00.
b.
2 gros mainan anak jika harga per unit Rp 7.500,00.
c.
5 kodi buku tulis jika harga per unit Rp 1.800,00.
3. Edi membeli satu
lusin buku tulis. Ia membayar dengan 3 lembar uang sepuluh ribuan dan mendapat
uang kembalian sebesar Rp3.000,00.
a.
tentukan
harga pembelian seluruhnya
b.
tentukan
harga pembelian tiap buku
c.
jika
Edi hanya membeli 8 buah buku, berapakah ia harus membayar?
4. Suli membeli barang-barang di Super
Bazar dengan rincian sebagai berikut:
20 mobil-mobilan dengan harga Rp. 60.000,
15 boneka dengan harga Rp. 75.000, 14 buku tulis dengan harga Rp. 35.000
a. Berapa rupiah yang harus dibayar
Suli seluruhnya?
b. Berapa banyak barang yang dibeli
suli?
c.
Jika suli
hanya ingin membeli 1 mobil-mobilan, 1 boneka, dan 1 buku tulis, berapa rupiah
yang harus ia bayar?
2.Harga
Pembelian, Harga Penjualan, Untung, dan Rugi.
Bu Siti membeli televisi
dengan harga Rp1.250.000,00. Sebulan kemudian televisi tersebut dijual dengan
harga Rp1.400.000,00. Dalam hal ini, Bu Siti mengalami untung Rp150.000,00. Jika Bu Siti hanya mampu menjual dengan harga Rp1.050.000,00, dikatakan Bu Siti mengalami rugi Rp200.000,00.
Dari uraian tersebut, dapat disimpulkan sebagai berikut.
a. Harga beli adalah
harga barang dari pabrik, grosir, atau tempat lainnya. Harga beli
sering disebut modal. Dalam
situasi tertentu, modal adalah harga beli ditambah dengan
ongkos atau biaya lainnya.
b. Harga jual adalah harga barang yang ditetapkan oleh pedagang
kepada pembeli.
Untung atau laba adalah selisih antara harga penjualan dengan harga
pembelian jika harga penjualan lebih dari harga pembelian.
Laba = harga
penjualan – harga pembelian
Rugi adalah selisih antara harga penjualan dengan harga pembelian
jika harga penjualan kurang dari harga pembelian.
Rugi = harga pembelian – harga penjualan
Contoh
1.
Seorang pedagang membeli jeruk sebanyak 40 kg dengan harga Rp6.500,00 per kg. Kemudian 30 kg di antaranya
dijual dengan harga Rp7.000,00 per kg, dan sisanya dijual dengan harga
Rp6.000,00 per kg.
Hitunglah
a. harga pembelian;
b. harga penjualan;
c. besarnya untung atau rugi dari hasil penjualan tersebut.
Alternatif Penyelesaian:
a. Harga pembelian = 40 x Rp6.500,00 = Rp260.000,00
Jadi,
harga pembelian jeruk adalah Rp260.000,00.
b. Harga
penjualan = (30 x Rp7.000,00) + (10 x Rp6.000,00)
= Rp210.000,00 + Rp60.000,00
= Rp270.000,00
Jadi, harga penjualannya adalah Rp270.000,00.
c. Karena
harga penjualan lebih dari harga pembelian, maka pedagang tersebut mengalami
untung.
Untung =
harga penjualan – harga pembelian
= Rp270.000,00 – Rp260.000,00
= Rp10.000,00
Jadi, besarnya keuntungan yang diperoleh
pedagang tersebut adalah Rp10.000,00.
3. Persentase Untung atau Rugi
1.
Menentukan persentase untung atau rugi
Persen
artinya per seratus.
Persen ditulis dalam bentuk p% dengan p bilangan real.
Dalam perdagangan, besar untung atau rugi terhadap harga pembelian
biasanya dinyatakan dalam bentuk persen.
Persentase untung = untung :
harga pembelian x 100%
Persetase rugi = rugi : harga
pembelian x 100%
Contoh :
Seorang pedagang membeli 1
kuintal beras dengan harga Rp6.000,00 per kg. Pedagang itu menjual beras
tersebut dan memperoleh uang sebanyak Rp620.000,00. Tentukan persentase untung
atau rugi pedagang itu ?
Alternatif Penyelesaian:
Harga pembelian = 100 x
Rp6.000,00
= Rp600.000,00
Harga penjualan = Rp620.000,00
Untung = Rp620.000,00 – Rp600.000,00
= Rp20.000,00
Persentase keuntungan pedagang itu adalah
Untung = untung : harga pembelian x 100%
=Rp20.000 : Rp600.000 x100%
= 3,33%
Latihan 2
1.
Seorang
pedagang membeli telur 10 kg dengan harga Rp 120.000, kemudian telur itu dijual
denan harga Rp12.500/kg. Berapakah keuntungan pedagang tersebut?
2.
Seorang
pedagang membeli telur 10 kg dengan harga Rp 120.000, kemudian telur itu dijual
denan harga Rp12.500/kg. Berapakah keuntungan pedagang tersebut?
3.
Sebuah
televisi terjual dengan harga Rp1.800.000,00. Jika penjual mengalami kerugian
sebesar 10%, maka berapa harga pembelian televisi tersebut?
4.
Seorang
bapak membeli sebuah mobil seharga Rp 50.000.000, karena sudah bosan dengan
mobil tersebut maka mobil tersebut dijual dengan harga Rp 45.000.000,.Tentukan
persentase kerugiannya!
5. Seorang pedagang
membeli gula 5 kg dengan harga Rp 65.000, kemudian dijual dengan harga Rp 15.000,
Berapakah besar persentase keuntungan pedagang tersebut?
2.
Menentukan harga penjualan dan harga pembelian
jika persentase untung atau rugi diketahui
Jika persentase untung atau rugi diketahui, kita dapat menghitung harga
beli atau harga jualnya.
Kalian telah mengetahui bahwa untung (laba) = harga penjualan – harga
pembelian, maka
a. harga
penjualan = harga pembelian + untung;
b. harga
pembelian = harga penjualan – untung.
Kalian juga telah mengetahui bahwa rugi =
harga pembelian – harga penjualan, maka
a. harga
penjualan = harga pembelian – rugi;
b. harga
pembelian = harga penjualan + rugi.
Catatan:
Dalam bentuk persen, harga beli dapat dianggap sebagai modal = 100%.
Contoh :
Seorang
pedagang menjual suatu barang dengan harga Rp210.000,00 dan mendapat untung 5%
dari harga beli. Tentukan harga beli barang tersebut.
Penyelesaian:
Harga
penjualan = harga pembelian + untung
Rp210.000,00 = harga pembelian + 5% harga pembelian
= 100% harga pembelian + 5% harga pembelian
= (100% + 5%) harga pembelian
= 105 : 100 x harga pembelian.
Harga
pembelian =Rp210.000 : (105: 100 )
= Rp210.000 x (100 : 105)
= Rp.200.000
Latihan 3
1.
Seorang
pedagang membeli ikan seharga Rp 50.000 / ekor. Jika pedagang tersebut
menghendaki untung 20 % berapa rupiahkah ikan tersebut harus dijual?
2.
Seorang penjual
telur memperoleh laba Rp. 5.500,00. Jika keuntungan itu 10% dari harga
pembelian, maka harga jual adalah . . .
3. Koperasi sekolah
membeli suatu barang dengan harga Rp500.000,00. Apabila koperasi sekolah itu
menginginkan untung 20%, maka barang itu harus dijual dengan harga...
4.
Hasil penjualan
suatu barang Rp. 108.000,00 dan ternyata mengalami kerugian 10%. Besar modal
pembelian barang adalah ...
5. Seorang ibu rumah tangga membeli satu lusin piring seharga Rp.
72.000,00. Kemudian ibu menjualnya kembali dengan harga Rp. 7.000,00 per
piring. Persentase keuntungan adalah ....
B. RABAT (DISKON), BRUTO,
TARA, DAN NETO
1. Rabat (Diskon)
Rabat artinya potongan harga
atau lebih dikenal dengan istilah diskon. Pernahkah kalian pergi ke swalayan
menjelang hari raya atau tahun baru? Biasanya menjelang hari raya atau tahun baru, toko-toko,
supermarket atau swalayan memberikan potongan harga untuk menarik para pembeli
yang akan berbelanja. Potongan harga inilah yang disebut rabat (diskon).
Biasanya diskon (rabat) ini diperhitungkan dengan persen.
Contoh :
Seseorang membeli baju di Toko Anugerah seharga Rp85.000,00. Toko
tersebut memberikan diskon 20% untuk setiap pembelian. Berapakah uang yang
harus ia bayar?
Alternatif Penyelesaian:
Harga pembelian = Rp85.000,00
Diskon 20% = 20/100 × Rp85.000,00
= Rp17.000,00
Uang yang harus dibayar = Rp85.000,00 – Rp17.000,00 = Rp68.000,00
Jadi, uang yang harus ia bayarkan sebesar Rp68.000,00.
Dari uraian di atas dapat
disimpulkan sebagai berikut.
Harga bersih = harga kotor – rabat (diskon)
dimana:
harga kotor adalah harga barang sebelum dipotong rabat (diskon).
harga bersih adalah harga barang sesudah dipotong rabat (diskon).
2. Bruto, Tara, dan Neto
Coba
perhatikan pada saat kalian membeli makanan kecil atau saat ibu membeli gula
pasir. Berat barang yang kalian beli merupakan
berat kotor, artinya berat makanan kecil ditambah berat
kemasannya. Berat kemasan barang seperti plastik, karung, kertas disebut tara. Berat barang beserta kemasannya
disebut berat kotor atau bruto, sedangkan berat barangnya saja disebut
berat bersih atau neto. Dengan demikian dapat disimpulkan sebagai berikut.
Bruto = neto + tara
Neto = bruto – tara
Tara = bruto – neto
Jika diketahui persen tara dan
bruto, kalian dapat mencari tara dengan rumus berikut.
Tara = persen tara x bruto
Untuk menentukan harga bersih setelah memperoleh potongan berat (tara)
dapat dirumuskan sebagai berikut.
Harga bersih = neto x harga/satuan berat
Contoh
Ibu membeli 5 kaleng susu.
Di setiap kaleng itu tertulis neto 1 kg. Setelah ditimbang ternyata berat
seluruh kaleng susu tersebut 6 kg. Berapakah bruto dan tara setiap kaleng?
Alternatif Penyelesaian:
Bruto setiap kaleng = 6 kg : 5 = 1,2 kg
Tara
setiap kaleng = 1,2 kg – 1 kg = 0,2 kg
Latihan 4
1. Bruto dari 6
kantong gula pasir adalah 180 kg dan memiliki tara sebesar 1,5%. Berat neto
dari masing-masing kantong adalah...
2.
Seorang pedagang
beras membeli 5 karung beras dengan harga Rp. 650.000,00. Pada masing-masing
karung tertulis bruto 50 kg dan tara 1%. Beras dijual dengan harga Rp. 2.000,00
per kg. Beras terjual semua, maka kerugian pedagang adalah ...
3. Dalam sebuah
karung yang berisi pupuk tertera tulisan berat bersih 50 kg sedangkan berat
kotor 0,08 kg, maka berat seluruhnya adalah . . . kg
4.
Pada karung tepung
terigu tertera tulisan; bruto = 46,5 kg, neto = 45 kg. Harga 1 kg tepung terigu
Rp. 4.200,00, harga bersih 1 karung terigu adalah ...
5. Seorang pedagang
membeli 2 karung beras masing-masing beratnya 1 kuintal dengan tara 2,5%. Harga
pembelian setiap karung beras Rp200.000,00. Sisa beras itu dijual dengan harga
Rp2.400,00 per kg, maka besar keuntungan adalah...
C. BUNGA TABUNGAN DAN PAJAK
1. Bunga Tabungan
Apabila
kita menyimpan uang di bank, maka kita akan mendapatkan tambahan uang
yang disebut bunga. Bunga tabungan dihitung berdasarkan persen nilai.
Bunga tabungan dihitung secara periodik, misalnya sebulan sekali atau setahun
sekali. Ada dua jenis bunga tabungan, yaitu bunga tunggal dan bunga majemuk. Bunga
tunggal adalah bunga yang dihitung hanya berdasarkan besarnya modal saja,
sedangkan bunga majemuk adalah bunga yang dihitung berdasarkan besarnya
modal dan bunga. Pada pembahasan ini kita
hanya akan mempelajari mengenai bunga tunggal.
Contoh :
Ayu menyimpan uang di bank sebesar
Rp2.000.000,00 dengan suku bunga 18% setahun dengan bunga tunggal.
Tentukan
a.
besarnya bunga pada akhir bulan pertama;
b.
besarnya bunga pada akhir bulan keenam;
c.
besarnya uang setelah 2 tahun.
Alternatif Penyelesaian:
Modal = Rp2.000.000,00; bunga
a. Bunga akhir bulan pertama
= (1/12) X (18/100) x Rp. 2.000.000
= Rp.
30.000
b. Bunga akhir bulan keenam
= (6/12) x
(18/100) x Rp 2.000.00
= Rp.
180.000
Bunga 2 tahun :
= 2 x (18/100)
x Rp 2.000.000
=
Rp 720.000
Jumlah uang seluruhnya
= Rp2.000.000,00 +
Rp720.000,00
=
Rp2.720.000,00
Jadi,
jumlah uang setelah 2 tahun adalah Rp2.720.000,00.
2. Pajak
Perhatikan setiap ibu kalian
membayar pajak listrik. Pajak tersebut biasanya dibayarkan setiap bulan.
Perhatikan pula saat kalian membeli barang, di setiap kemasannya biasanya
tertera tulisan harga ini sudah termasuk pajak. Jadi, menurut kalian, apa sebenarnya pajak itu?
Pajak adalah suatu kewajiban yang
dibebankan kepada masyarakat untuk menyerahkan sebagian kekayaan kepada negara
menurut peraturan-peraturan yang telah ditetapkan pemerintah.
Jadi, pajak bersifat mengikat dan memaksa.
Banyak sekali jenis-jenis
pajak, antara lain Pajak Bumi dan Bangunan (PBB), Pajak Pertambahan Nilai
(PPN), dan PajakPenghasilan (PPh). Perhitungan nilai pajak akan kalian pelajari
pada bagian ini.
Contoh :
Pak Putu memperoleh gaji Rp950.000,00 sebulan dengan penghasilan tidak
kena pajak Rp380.000,00. Jika pajak penghasilan (PPh) diketahui 10%, berapakah
besar gaji yang diterima Pak Putu per bulan?
Alternatif Penyelesaian:
Besar gaji = Rp950.000,00;
Penghasilan tidak kena pajak = Rp380.000,00
PPh = 10%
Besar penghasilan kena pajak
=
Rp950.000,00 – Rp380.000,00
=
Rp570.000,00
Besar pajak penghasilan = 10% x penghasilan kena pajak
= (10/100) x Rp570.000
= Rp 57.000
Gaji yang diterima = Rp950.000,00 – Rp57.000,00 =
Rp893.000,00
Jadi, besar gaji yang diterima Pak Putu per bulan adalah
Rp893.000,00.
Latihan 5
1. Nania menabung
uang di bank sebesar Rp2.000.000,00 dengan bunga 8% setiap tahun. Setelah 9
bulan, uang tabungan Nania menjadi...
2. Rio menabung
dibank sebesar Rp 75.000 dengan bunga 12% per tahun. Hitung jumlah uang Rio
setelah enam bulan.
3. Seorang ibu
mendapat gaji sebulan sebesar Rp 1.000.000 dengan penghasilan tidak kena pajak
Rp 400.000. jira besar pajak penghasilan (PPh) adalah 10 % berapakah gaji yang
diterima ibu tersebut?
4. Ahmad membeli
sepeda motor dengan harga Rp 15.000.000 dengan pajaknya 10 %, setelah beberapa
tahun Ahmad menjual mator tersebut dengan harga Rp 11.500.000. berapakah
kerugian yang diderita Ahmad?
5 Bu Zainab seorang peternak ayam
potong. Untuk memperluas usaha ternak ayamnya, ia meminjam uang pada koperasi
“Setia Kawan” sebesar Rp. 2.400.000 dengan bunga pinjaman 12% per tahun selama
10 bulan. Berapa uang cicilan yang harus dibayar oleh Ibu Zainab setiap bulan?
EVALUASI
Jawab pertanyaan-pertanyaan di bawah ini
dengan tepat!
1.
Pak Hamid menjual sepeda motor seharga
Rp. 10.800.000,00 dengan kerugian 10%. Harga pembelian sepeda motor Pak Hamid
adalah …
2.
Seorang pedagang membeli 24 kg jeruk seharga Rp
150.000,00. Setengahnya ia jual dengan harga Rp 9.000,00 per kg, sepertiganya
ia jual dengan harga Rp 7.500,00 per kg, dan sisanya ia jual dengan harga
Rp 6.000,00 per kg. jika seluruh jeruk terjual habis, hitung untung atau rugi
pedagang tersebut?
3.
Sebuah tape recorder dibeli dengan harga Rp500.000,00.
Agar harga jual mendapat untung 35%. Hitunglah harga jual tape recorder.
4.
Janu mendapat untung 25% dari penjualan
motornya. Ia menjual motor tersebut dengan harga Rp. 625.000,00. Berapa harga
pembelian motor tersebut?
5.
Setengah lusin sepatu dibeli dengan harga Rp
450.000,00. Jika untung yang diinginkan 20%, hitung harga jual sepasang sepatu?
6.
Sebuah komputer bekas diperbaiki dengan menghabiskan
biaya Rp 200.000,00. Jika komputer tersebut dijual dengan harga Rp
1.200.000,00, maka akan memberikan keuntungan 20%. Hitung harga beli komputer?
7.
Diketahui harga sepasang sepatu sandal Rp 68.000,00.
Jika diberi diskon 25%, hitunglah harga sepasang sepatu sandal setelah di
diskon!
8.
Bruto satu dus barang adalah 48 kg. Jika taranya 2,5%,
hitunglah berat bersih (neto) satu dus barang tersebut!
9.
Andi menabung uang sebesar Rp800.000,00
di Bank dengan bunga 6% per tahun. Jumlah tabungan Andi setelah 9 bulan adalah
...
10. Nina
menabung Rp. 250.000,00 disebuah bank dengan bunga 18% per tahun. Bunga yang
diperoleh Nina sesudah 10 bulan adalah ....
Langganan:
Komentar (Atom)